LoRAs as Composable Programs

There is a growing trend to think of large language models (LLMs) as operating systems (OS). They have the ability to read and write to short-term memory in the form of their context, as well as use tools to connect them to other applications. Particularly prevalent in the age of expensive pre-training, I think an interesting discussion revolves around finetuning, which now represents the vast majority of the LLM community these days.

Thinking about the base model (eg GPT or Stable Diffusion) as an operating system, others build on top of this system by writing “programs”. For instance, on top of such an operating system, one might “write” a LoRA, a vision adapter (ex. LLaVA), or a ControlNet on top of the OS. Crucially, these programs only work with the particular OS they were trained on, as they interface with the specific embedding space* of the base LLM.

There are some really interesting questions to me:

1. What types of programs might we like to write?
2. How will these programs interface with each other?
3. How can we “merge” code into single programs?
4. Finally, how can we ensure backwards compatability with these programs?

* By embedding space, I refer to the “meaning” of the latent embedding $z$. There is some mapping between the neural network input $x$ to embedding $z$ to output $y$. I argue the mapping from $z \to y$ is “mostly” the same after finetuning (empirically), but finetuning mostly changes $x \to z$ so that we find the right embeddings $z$ for the new task.

What types of programs might we like to write?

Finetuning of base models is incredibly popular: you can see thousands of finetuned models on websites such as Huggingface or Civit AI. Generally, you might want such a model because:

1. You want the model to be specialized. At inference time, the model costs money and time ~proportional to the number of weights it has, and you want all those weights to be useful for your task; eg, you should not waste inference for a roleplay model that is only useful for math or coding.
2. You want to teach the model something new. This can range from continual learning (teaching the model new world events after its pretraining date), to new content (a database or task the model wasn’t pretrained on), to specific characters (ex. teaching the model to generate you or a celebrity), and more. This is particularly relevant for personal or enterprise data, which should never be publicly available, including when abstracted away by the open-source weights.
3. You want give the model a new interface: LLMs do not inherently understand images, but you can adapt an LLM to do so with a vision encoder (LLaVA); image generators are trained with only text conditioning, but can be taught 2D conditioning (ControlNet).
4. You want the model to forget bad behaviors. This encompasses ideas such as RLHF (Unifying RLHF Objectives) as well as model editing, where you try to identify where an (incorrect) fact is stored in the model, and then delete it by editing the weights. This mimics conventional cybersecurity with iterative cycles of vulnerability discovery and continual patches.
5. You want the model to run faster. You could do this by removing unnecessary weights (pruning/quantization), or by doing something more drastic such as replacing a slow attention layer with a faster approximation, or teaching the model to “plan faster” with techniques such as Consistency Models.

One argument to be made is that – perhaps – LLMs will be able to absorb all necessary information in-context without finetuning (ie, the “RAM”), and so editing the model weights (the “hard drive”) will not be necessary. However, given the broad scope of capabilities above, I think finetuning models will continue to be popular for a long time to come.

How will these programs interface with each other?

At a more technical level, many fine-tunes nowadays are additive on top of the embedding space defined by the base model; I focus on two here. In particular, suppose that at some layer $l$, the base model has a matrix multiplication $W_l$ (which represents the “code” of the OS):

Many models compose these layers in the form of attention layers – which “read in” the input – and large feedforward layers – which are “queried” by the attention layers and act as a large “database”. (Note I omit the nonlinearity in the above equation.)

LoRA

Many finetuning methods are based upon low-rank adaptation (Edward Hu et al. 2021), which builds on older work on adapter modules (Neil Houlsby et al. 2019). These methods learn two lower-rank matrices $L_l$ and $R_l$ such that the shape of $L_l R_l$ is the same as $W_l$. Then, the new model is:

Crucially, these weights can be merged with $W_l$ at inference time as $\tilde{W}_l = W_l + L_l R_l$, which incurs no extra inference cost.

Additionally, if the rank of the new matrices is much lower than the rank of the old matrices, we might consider that the new model is “mostly the same” as the base model, and it keeps the old embedding space, but applies a new transformation to it at each layer. This might be true even if the rank is not small (Jonathan Frankle et al. 2020).

It is common nowadays to only apply LoRAs to the attention layers, which generally affects the “querying” behavior of the model; in some sense, they are telling the CPU “where to look”.

ControlNet

At a high level, a ControlNet (Ethan Perez et al. 2017; Lvmin Zhang et al. 2023) is an additional module which looks like:

where the $*$ operation is element-wise with some new learned weights $w_l$. As $CN$ can be some arbitrary function, it is not possible to perform the merge like a LoRA, but instead the ControlNet costs extra inference time and memory.

Since these modules are additive, we can have many such programs $f^i$ on top of the same base model:

and then the program $i$’s output at one layer $f^i_l$ will interface with program $j$ by modulating the input $z_{l+1}$ to the next layer, which is the input to $f^j_{l+1}$. If the embedding space $z$ is a subset of the distibution $f^i$ is trained on, then the learned transformation $f^i$ should still “work”.

Other Methods

Although I focus on LoRAs and ControlNets, there are several other interesting finetuning methods:

1. Prompt tuning (Taylor Shin et al. 2020; Brian Lester et al. 2021; Rinon Gal et al. 2022): instead of changing the weights of the neural network, learn a “prefix” (ie, to prepend to the prompt) at the input $x$ of the model. Intuitively, this finds the right embedding in the mapping $x \to z$ that represents the task. This can also be done with a different modality as the base model (Maria Tsimpoukelli et al. 2021; Haotian Liu et al. 2023).
2. Learning scale/shift parameters (Jonathan Frankle et al. 2020; Kevin Lu et al. 2021): finetune only the “normalization” scale/shift parameters, akin to $w_l$ in the equation above. This shifts where the embeddings are in the space without changing the transformations applied to them.
3. Model editing: identify where a “fact” is stored in the neural network (typically in the feedforward “database” layers), and directly delete it in the weight space.

How can we merge programs?

A very curious observation to me is that you can combine these LoRAs and ControlNets together, and it works! For instance, start with Stable Diffusion and take both a pretrained LoRA and a pretrained ControlNet. This yields:

Both the LoRA and ControlNet are trained separately, ie. on top of the weights and corresponding embedding space of the base Stable Diffusion. And yet, they work together!

I think this means the embedding space is not really changed by these methods: rather, they are learning to transform inputs to different parts of the high-dimensional embedding space, that the different modules still know how to interpret. In this sense, all modules trained on top of the same OS “agree” to use the same protocols for reading bits.

I think this is a very nontrivial observation. These models are not finetuned on top of each other; they are finetuned independently to simply maximize their own objectives, and yet we have this “emergent” behavior that they still empirically both do their own things correctly when added on top of each other.

Furthermore, the ability to “git merge” models has been a longstanding dream of deep learning, particularly among decentralized open-source communities – in a general sense, it enables tremendous possibilities with training different models by different people on different datasets.

SVD Perspective

For simplicity, going forwards, I will write $W^i = L^i R^i$.

It is trivial to consider a counterexample where two LoRAs would cancel each other out: simply set $W^1 = - W^2$, and then $\hat{W} = W + W^1 + W^2 = W$, thereby destroying the information from the finetuned LoRAs. More generally, one might measure the “conflict” between two LoRAs with some notion of distance between $W^1$ and $W^2$.

Consider the SVD transformation $W = UDV^T$. The range of a LoRA layer is defined by read-out matrix $V^T \approx R$, and the embedding spaces it expects to operate on are defined by the read-in $U \approx L$ (“eigenfaces”).

If $W_l + U^2_lD^2_l(V^2_l)^T$ happens to move the embeddings (after the nonlinearity) into the null space of $U^1_{l+1}$, we should expect $W^1$ to break. Since $U^1_{l+1}$ was trained on top of $W_l$, we expect the range of $W_l$ to not interfere with $U^1_{l+1}$, and so this requires the range of $(V^2_l)^T$ to match the null space of $U^1_{l+1}$.

In contrast, if $(V^2_l)^T$ is mostly orthogonal to $U^1_{l+1}$, perhaps maybe these LoRAs can operate independently without interference!

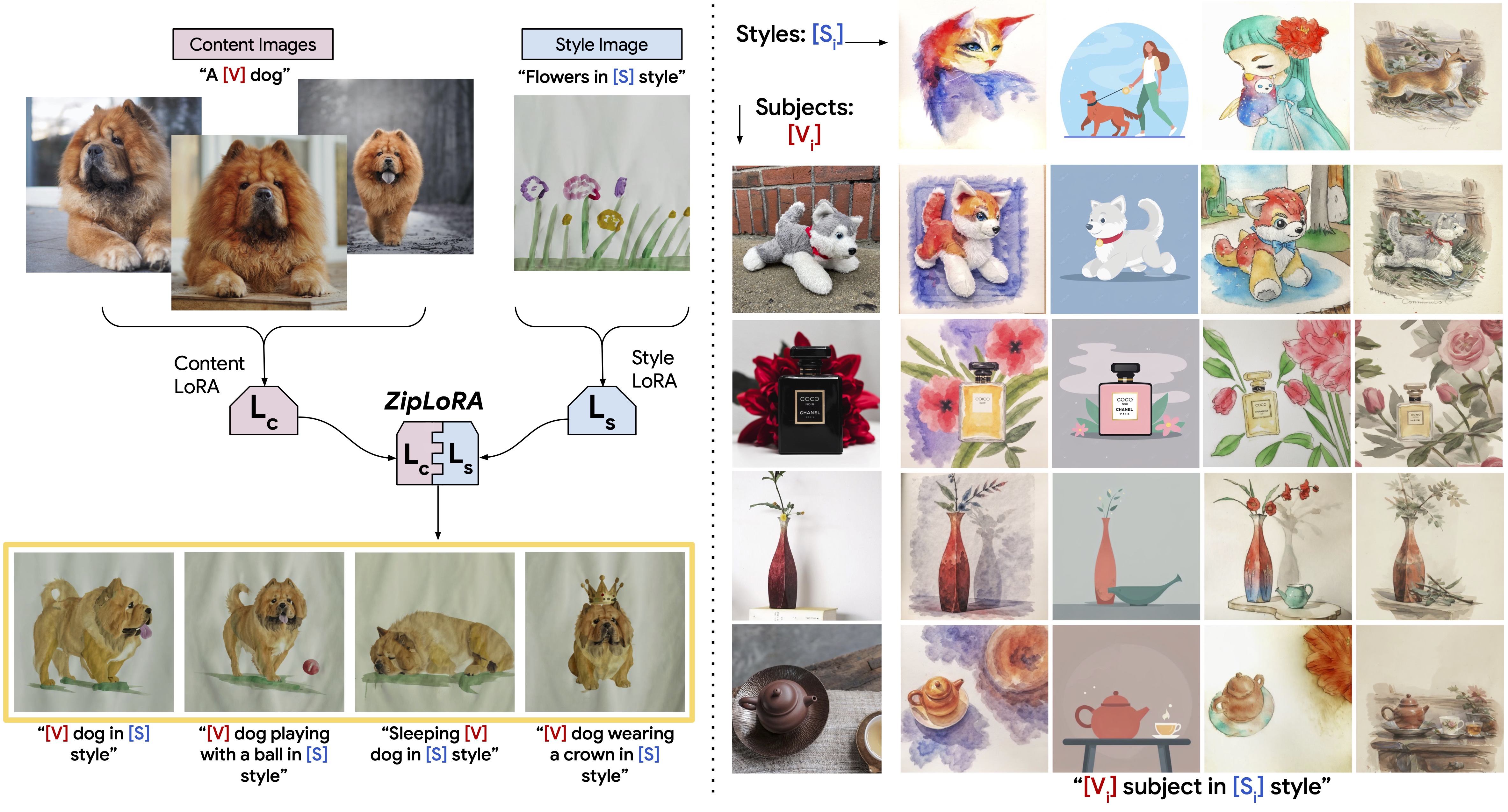
ZipMerge

Viraj Shah et al. 2023 consider the Frobeninus norm as a notion of distance:

They propose a merging procedure for two LoRAs where they minimize this norm, and empirically show that the new merged model as a Frobenius norm close to zero, and is preferred by humans a majority of the time compared to a naive merge (although I think in practice, users like to sweep the merge weights, so the result is not as drastic as shown in the paper).

Their method creates a pretty 2x2 grid showing merging “style” LoRAs with “subject” LoRAs:

An interesting observation is that the Frobenius norm (cosine similarity), when viewed at a per-layer level, is high at the start and end of the network, and low in the middle:

We can further consider the attention matrix $K$ to act like the read-in matrix $U\approx L$, and the matrix $V$ to act as the read-out matrix $V^T \approx R$. We can see the read-in matrices – the ones which interpret the embedding space – have lower conflict than the read-out matrices (even without the ZipMerge procedure, represented in blue).

Git Re-Basin

Samuel K. Ainsworth et al. 2022 directly merge the weights of $W^1$ and $W^2$ with a linear interpolation – i.e. $\tilde{W} = \lambda W^1 + (1 - \lambda) W^2$. They find this has good performance only after accounting for the permutation of the neural network weights across the layers.

People in the community often do this kind of interpolation for language models and Stable Diffusion without the permutation (see eg, the github repo mergekit), but sometimes this is done with spherical interpolation instead (SLERP). The work by Jonathan Frankle et al. 2019 suggests the permutation might be fixed early on in training, and thus different finetunes on top of the same base model might have the same permutation anyhow.

Mixture of Experts

A common technique nowadays is to have multiple “experts”, of which a subset are called upon at inference time based on their perceived expertise relative to the inference query. At a high level, we can view this as moving the abstraction into the network:

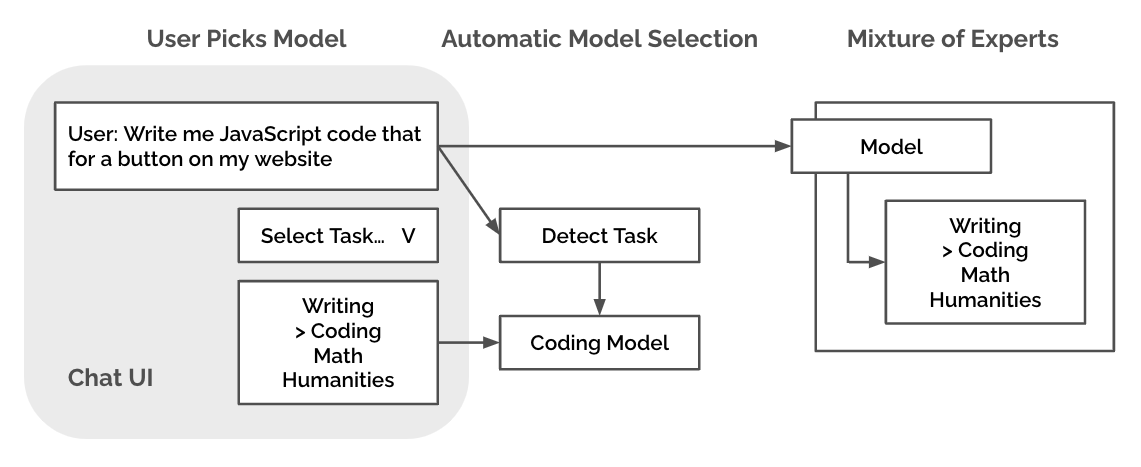
In practice, these experts are only used in the feedforward layers, which is the opposite of what the LoRAs are commonly applied to. However, we can consider a similar notion of embedding space for these feedforward layers.

Frankenmerging

“Frankenmerging” is an informal term for a merging technique described as an “affront to god”. Rather than linearly merging the weights, different layers are concatenated together to create a new model which is deeper than the original models. For example, Goliath-120B merges two 70B LLaMa-2 models by carefully selecting a schedule of layers from those two models.

Naturally, you might think: how can this work! This only makes sense at all because of the skip connections (and layer dropout, where training randomly drops layers p% of the time). And if you consider the embedding space is defined by the base model, and the finetunes perhaps don’t destroy the embedding space, maybe the layers are… composable transformations of that embedding space?

Generally, these methods pick one base model to comprise the early and final layers, and do the frankenmerging only in the middle, which I think has a similar intuition to the graph in ZipLoRA: perhaps the conflicting parts of the finetuned models are these early read-in and late read-out layers, and the middle parts are not too conflicting. Maybe the OS should also come with a protocol for these*?

*Note LLMs have tokenizers and Stable Diffusion has a VAE, which is already a little like this.

How can we ensure backwards compatability?

One of the benefits of doing your work on an open model rather than training your own LLM with your desired fancy architecture and perfect training parameters is that you can utilize programs the open-source community develops, alongside yours. For instance, if you train an image content LoRA to generate a particular object, you could then also use style LoRAs or ControlNets to have more control over the image generation.

Now, what if the OS (or another program) gets an update? Typically, these updates are direct finetunes over all the weights (conceptually the same as a high-rank LoRA), or sometimes just a new model entirely. A lack of backwards compatability can delay adoption: for instance, one of the reasons Stable Diffusion 1.5 is still popular over the newer SDXL is due to all the programs written on top of SD1.5.

I mean, in some sense, we’ve seen that it “just works” to add programs together, or even frankenmerge them, so if you think of the delta of a newer fine-tuned version of a model as such a program, then maybe it “just works”? Should we constrain OS updates to some form? What are the boundaries of this conceptual framework, and how does the rank of the LoRA affect interference? What if we want to make an architectural change, eg. to make the model faster?

I think more generally, we need to consider that our pretrained models will be around for a long time (Microsoft supports a Windows version for 10 years) – both due to the obvious pretraining cost but also the programs built on top of them – and we should try and train these OS models in such a way that programs can composably be built on top of them.