Spending Inference Time

Inference is king: at the end of the day, the user wants a mapping from the input query to their desired output. While the two big ideas from The Bitter Lesson are learning (~= training) and search (~= inference), at the end of the day, people don’t really care about how much the model cost to train. But they will measure how slow the model is to milliseconds and put up the API cost on big leaderboards. If you tell the user it will take 5s but they have to wait 10s, they will end up leaving and not coming back.

So, how should we think about getting the most bang for our inference buck? Traditionally, search has been very powerful, leading to AI’s superhuman capabilities (DeepBlue, AlphaGo). Nowadays, the model’s forward pass alone can even be prohibitively expensive, and the open-source community frequently tries to fit models into consumer GPUs (eg, Stable Diffusion).

I think inference is really interesting because:

  1. The time we wait for the model output is human time, which is real time
  2. From a business perspective, the fundamental interest is the cost/time to achieve certain performance
  3. There are so many design decisions on how to spend inference compute
  4. And search is such a powerful idea! For example:

Framework

At a high level, inference typically has two key components – a model generating sample candidates and a form of ranking for those candidates – which eventually lead to the final result. We can view the y-axis as time, and the 2D area of these processes as the compute spent:

The degree to which we can parallelize the model affects the exact tradeoff of time and compute, but generally we think of them as being proportional. The model might also consist of a search procedure, and so the API/UI might not literally return the output of the neural network to the user.

Breadth-sampling

A very common usecase consists of the model generating multiple outputs, and the user picking the best one. For instance, many image geneartors such as Midjourney shows the user four images, and then the user selects one (to upscale, or to show to others). Similarly, one might ask an LLM to generate an answer several times, and then pick the best one for their application.

Best-of-n sampling

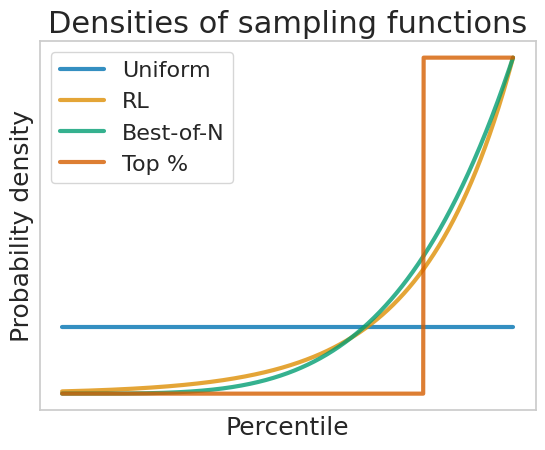
Here, the ranker is human, which we might approximate as the ground truth ranker / reward. Typically, the draws from the model are performed uniformly at random (but not necessarily). In a pairwise matchup between two settings – one with $n$ draws and the other with $m$ – the former will have a winrate of $\frac{n}{n + m}$. If $n = 3m$, this implies a 75% winrate, which is pretty big!

This represents a breadth search: we are sampling the same thing from the model. Typically, this can be parallelized, which incurs no time (but does cost more). And this also incorporates elements of design: in almost the UI alone (and a little extra cost), we can get the user to a much better result with very little effort on their end.

In reality, humans are not “ground truth”. It is suggested humans disagree with each other on pairwise rankings about 20% of the time (depends a lot on the dataset and task). We might thus also consider a “noisy” oracle which scales the prior $\frac{n}{n+m}$ by 20%.

Approximate ranker

However, human ranking isn’t free! Image-generating users might find more than 4 images at once overwhelming; language-generating users can typically read at about 200 wpm (in English). Thus we may try to rank the sample candidates ourselves before showing them to the user, particularly in language. Typically, this is done using a trained reward model trained either on pairwise classification or Elo-style reward modeling.

In Reiichiro Nakano et al. 2022, they estimate the human preference when using a learned reward model as a ranker. I also consider scaling curves from Leo Gao et al. 2022, using the elo-based winrate implied by their reward model (comparing a 1.2B parameter reward model and a 12M one):

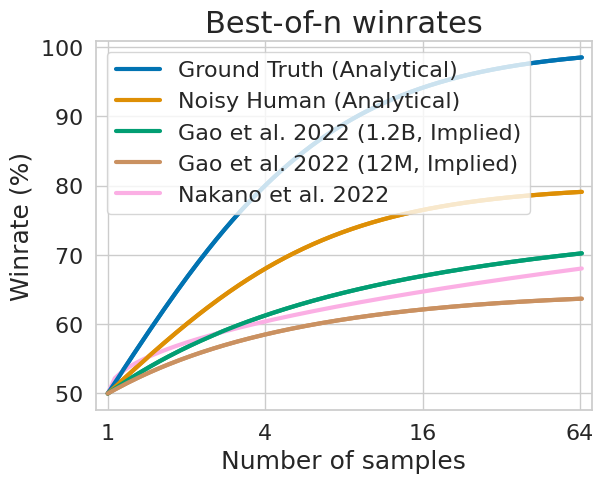
We can see the approximate ranker hurts a lot, but using a better ranker can get closer to the noisy-human oracle. If we have extra compute to spare, we might first draw many samples from the model, then pick the best few using our reward model, and finally have the user pick amongst those.

Training vs inference

Quite interestingly, we can also tie together training and inference this way: since larger models perform better at inference, and they cost more / take longer at inference, we can relate the cost of training a larger model with the comparative inference benefit from it. On Chatbot Arena, GPT-4 has a 75% winrate against GPT-3.5, which is the same as our implied 3x oracle winrate above!

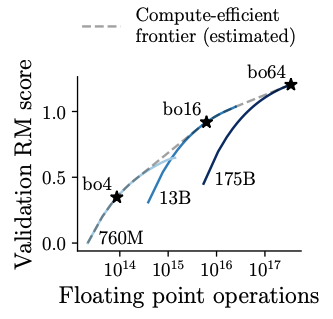
Back in Reiichiro Nakano et al. 2022 for language, they find that to maximize performance given an inference-flop budget, the answer is not to simply pick the biggest model available. For instance, best-of-16 13B outperforms best-of-1 175B when using learned reward models:

Tree of Thoughts corroborates this with modern models (and tree search, below), for the Game of 24:

  1. GPT-4 by itself (13 cents) has a success rate of 7.3%
  2. GPT-3.5 with search (~8 cents total) has a success rate of 19%

Depth-sampling

We can extend the search setup as a depth-wise procedure, where we alternate between best-of-n sampling, choosing the best one, and then performing new best-of-n sampling on top of the previously chosen sample. This create trees, with sampling generating children from parent nodes.

Tree search is traditionally studied in the context of board games such as chess, where different board states are considered after action nodes. As described in the introduction of this blog, tree search is immensely powerful: even with all our new machinery, the neural networks of today still do not match the performance of AlphaZero with search, despite our now-massive networks and almost a decade of new research.

This was studied for board games in Andy L. Jones 2021, which finds increasing training compute linearly roughly corresponds with decreasing inference compute by the same factor, in the 9x9 Hex board game:

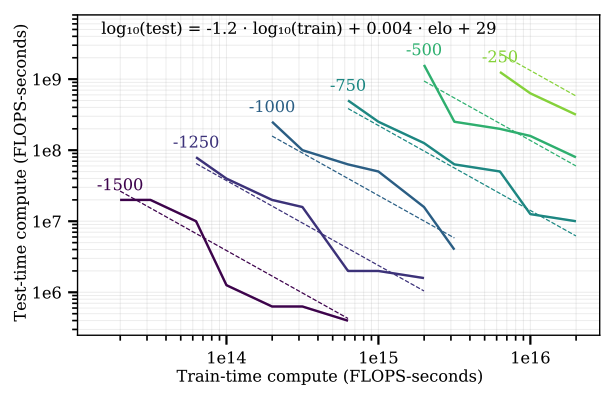
Additionally, the scaling law aligns very closely with the “ground truth” scaling law above (2x compute for $\frac{2}{2+1} = 67\%$ winrate), highlighting the notion the model has learned a very good reward model (it pretty much solves the board game).

Instead of a ranking model, what if we just asked the human to rank? In image generation, it is common for the user to then take the best image and “remix” it into new images, forming a sort of genetic lineage for AI images:

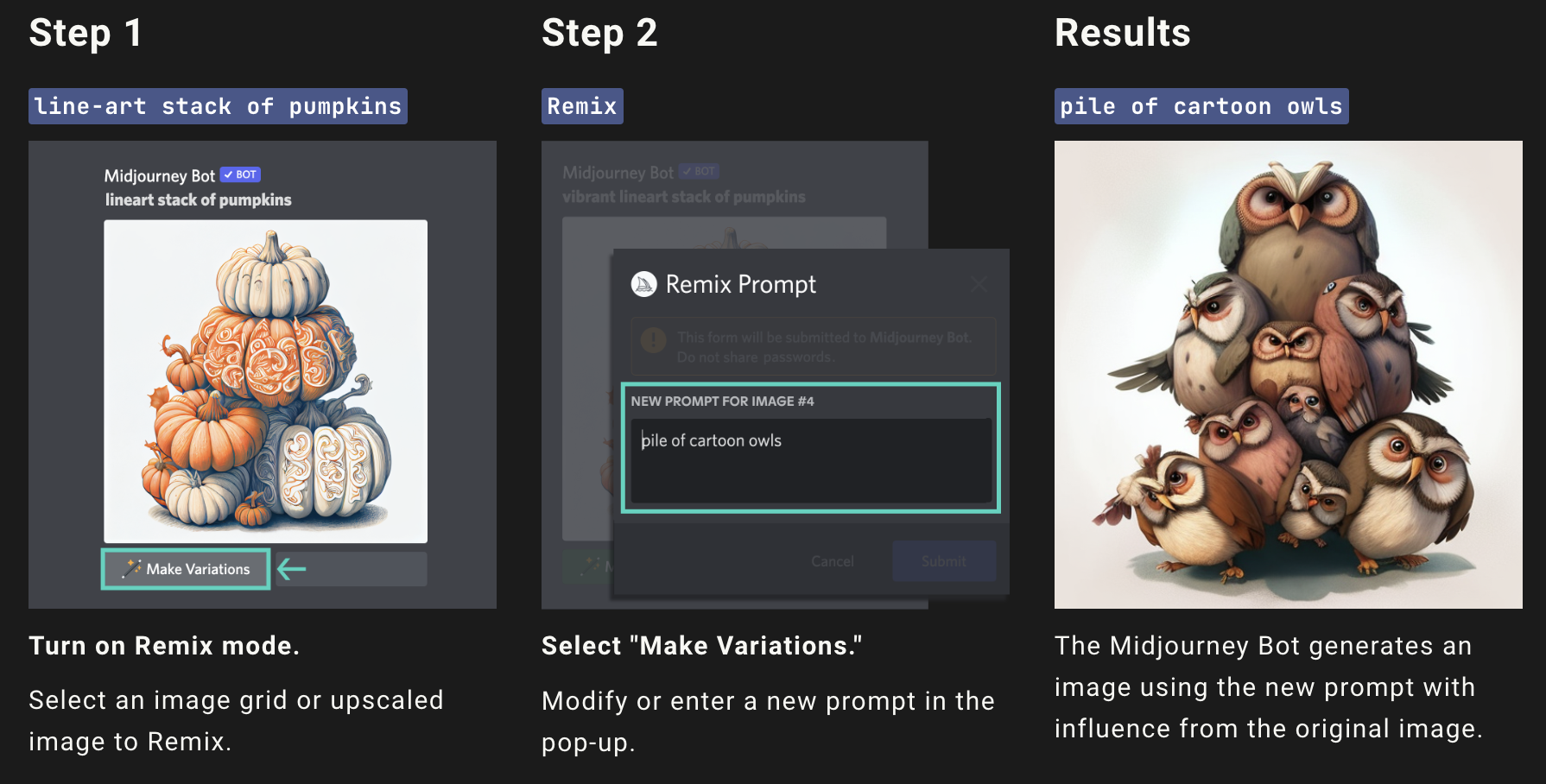
When you include all the ways to edit an image (remix, inpainting, sampling, …) some users spend hours to produce single images. This is sort of like how an artist or musician might develop their own pieces, by iteratively improving on their work using an instrument – but this requires the feedback from the tool to be fast, and fun to use. However, if the tool is too slow or cumbersome, the user will simply walk away after the first query: this is why we must place a high value on inference time to design a good product.

I think this is a very powerful idea tying together product design and model capabilities, and is an interesting direction for developers to optimize.

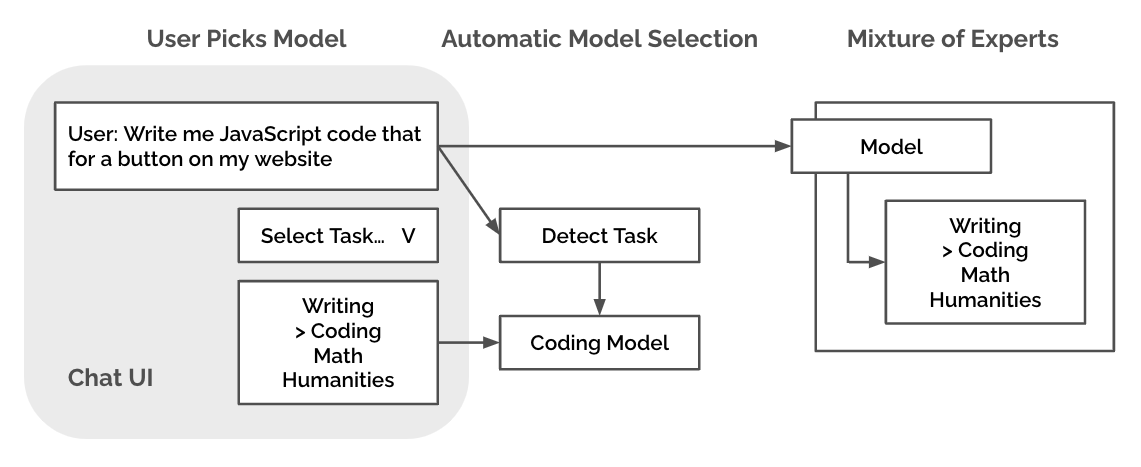
Mixture-of-experts

One way to perform search within the model itself is mixture-of-experts, famously implemented by Mixtral, which has around 47B parameters but can be run at the inference cost (and time) of a 13B model. It does this by dynamically selecting which parts of the model to use per inference query. On Chatbot Arena, it has better performance than many 33B open source models, and a comparable elo to more expensive closed-source APIs.

See also LoRAs as Composable Programs:

Other techniques

There are many other approaches to search, to name a few:

  1. Diffusion allows models to iteratively update an image during generation, and can be dynamically varied per the inference budget (and users typically do, in human-tree loops).
  2. Model predictive control from robotics also has iterative model updates, and dynamic inference budget.
  3. Deep Equilibrium Models run the model iteratively until the output has converged; the compute can thus vary dynamically depending on how much “thinking time” is needed per the specific query.
  4. Chain of Thought also allows language models to dynamically vary the compute based on the query by providing the model with a “scratchpad” to show its work.

Training-time optimizations

Although above we discussed how increasing training compute could be compared to increasing inference compute, we can also consider methods which increase training compute but do not increase inference compute.

Overtraining

The Chinchilla work famously described the optimal scaling laws for language models based on training compute. Thus given we care about inference compute, we should imagine the inference-optimized training compute should be shifted for a given model size compared to the Chinchilla law: the “overtrained” regime. I will consider extending pretraining time to just be the “pretraining” stage of training, and instead discuss additional finetuning stages that enable us to train a “better” model.

Distillation

Distillation is a field chiefly concerned with this question: how can we have a small model approximate the outputs of a larger, more expensive model? Typically, this is performed by setting up a new training objective where the model (the “student”) predicts the outputs of either a larger model or expensive search procedure (the “teacher”).

While difficult in general, there are a few overarching threads of research:

  1. Data augmentation: the teacher can generate data for the student to train on, identically to pretraining.
  2. Soft labels: the student trains to match the teacher’s confidence on the labelled output, a strict superset of data augmentation which requires access to the probabilities the teacher assigns to possible outputs. The hope is this additional information vs the raw dataset can help the student learn “better”.
  3. Architecture distillation: the student uses a faster architecture (ex. RNN or sub-quadratic attention mechanism) than the teacher (typically a transformer). The hope is that if the architecture is the same size, it could simply be faster by replacing the slow attention mechanism, reducing inference compute.
  4. Planning distillation: the student tries to match the teacher planning algorithm, common in tree search (the student tries to predict the final output of the tree search), as well as diffusion (Consistency Models).

Although these approaches generally do not achieve perfect parity with the teacher, we can then wonder:

  1. Can we recoup the inference cost to use a larger model? Combine with search tools?
  2. Can we use these faster methods to help form effective human-tree searches?

Task-specific finetuning

Both model and planning distillation are hard, so another popular approach is task-specific finetuning. The idea is that the model has been pretrained to perform a large amount of tasks, but the end user generally only cares about one or a subset of those tasks, and so any compute that is not being used directly for their task is wasted. A super-simple version of this is that the pretrained model can be finetuned only on “helpful” training data: this is often called supervised finetuning in chatbot literature.

More generally, it is common to train roleplay, coding, or math-specific models (to name a few tasks). It is not really easy to get task-specific models through API providers at the moment, but many open-source finetuned models can outperform significantly more expensive closed-source APIs at specific tasks. We can also think of this as a “hard” version of mixture-of-experts, where expert selection is exposed to the user.

RLHF

Related to reward modeling is Reinforcement Learning from Human Preferences (see Unifying RLHF Objectives), which seeks to adapt the language model to optimize for the same reward model as best-of-n sampling, but without the additional inference cost. Generally, RL methods try to learn a policy $\pi_\theta(x) \propto \beta e^{-\frac{1}{\beta}r(x)}$. Assuming perfect optimization, we can visualize the sampling distribution of the policy (treating reward as percentile):

Thus if we learn the policy correctly, we can approximate the best-of-n distribution with a single forward pass. $\beta$ trades off learning an aggressively high $n$ with practical feasability and overfitting. And in practice, this is typically a very effective distillation procedure: for example, the Direct Preference Optimization work finds RL is comparable to best-of-128 sampling on Anthropic-HH – a 128x reduction in compute!

However, RLHF typically reduces the variance of the model, and so does not benefit from further best-of-n (these tricks don’t stack). We might think of the offline setting (one round of RLHF on the preference dataset) as approximating the best-of-n sampling procedure*.

Ongoing research in RLHF studies online (iterative) RLHF, which performs multiple rounds of RL. The ending policy of each round is used to initialize the next round of RL – a form of tree search, like above! Methods like ReST (and OpenAI’s own PPO) are still new, but offer the promise to improve meaningfully on top of best-of-n (in addition to simply distilling it), much as tree search powerfully improves learned policies in board games.

* They are not exactly equal. If we model reward function noise as iid, best-of-n sampling with a proxy reward will always suffer a noise penalty, whereas RLHF might be able to average out the noise over many training examples, and thus yield better performance with a good enough dataset.

Commentary

Clearly, there are many axes upon which we can maximize the use out of our inference budget which are not simply model size. However, there are many interesting questions to continue to consider for your use-case:

  1. Mostly we’ve been concerned with inference compute by itself, but the real valuable resource is human (~= inference) time. How do our approaches change based on our parallelization ability and cost?
  2. How can we design user interfaces, and our models with them, such that we can incorporate the end user into an effective human-tree search procedure?
  3. How much do we value inference cost? If an inference FLOP is worth a training FLOP (one-time discoveries, like scientific research), this greatly shifts the allocation of time we should spend towards training.
  4. What are the limits of training-time optimizations? Where are the fundamental limits, and how close can we get to achieving them?

I think this is a really exciting direction, and look forwards to future work along these axes.

Notes mentioning this note

There are no notes linking to this note.